SPH Fluid Simulation
INTRODUCTION
Smoothed-particle hydrodynamics (SPH) is a meshfree, particle method originally used for continuum scale applications. It was first invented by Gingold and Monaghan and Lucy to solve astrophysical problems. It has been used in many fields of research, including astrophysics, ballistics, volcanology, and oceanography.
In SPH, the state of a system is represented by a set of particles, which possess material properties and interact with each other within the range controlled by a weight function or smoothing function. Problems arise when rest densities and masses of neighboring particles vary within the smoothing length, as in such cases the smoothed quantities of a particle show falsified values. Such problems can be observed near the interface of multiple fluids with density contrasts.
In the paper I read, the authors present a formulation based on SPH which can handle density discontinuities at interfaces between multiple fluids correctly without increasing the computational costs compared to standard SPH. The basic idea is to replace the density computation in SPH with a measure of particle densities and consequently derive new formulations for pressure and viscous forces.
Density
The idea is to make each particle treat its neighbors as if they would have the same rest density and mass as itself. The particle density δ of a particle is defined as
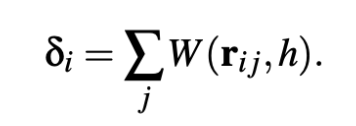
Then compute the adapted density ρ˜ of a particle by multiplying the particle density by the mass of
the particle
Pressure
Replace the standard SPH density ρ with the adapted density ρ˜ introduced above, yielding the
following equation for the pressure p˜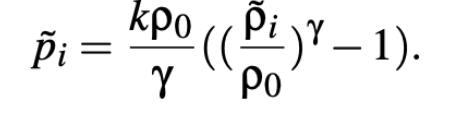
Pressure Force
In the standard approach, replace ρ by ρ˜ and p by p˜, yielding the pressure force of the particle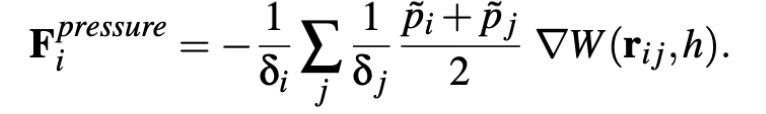
Adapt Monaghan’s pressure force equation, yielding the pressure force of the particle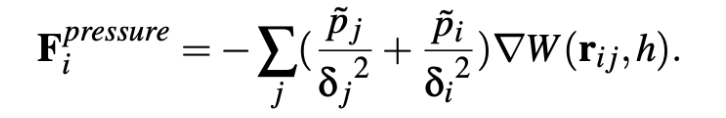
Viscous Force
Adapt the viscous force equation, yielding the pressure force of the particle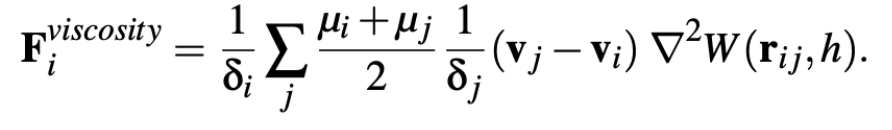
Results
In order to more intuitively observe the difference between the former SPH and the adapted SPH, I applied both solutions for the liquids simulation. The left side animates as the former SPH and the right animates as the adapted SPH.
The use of the former SPH produces
a spurious interface tension and a gap between two fluids with a density contrast(left), while the
new approach acts properly(right).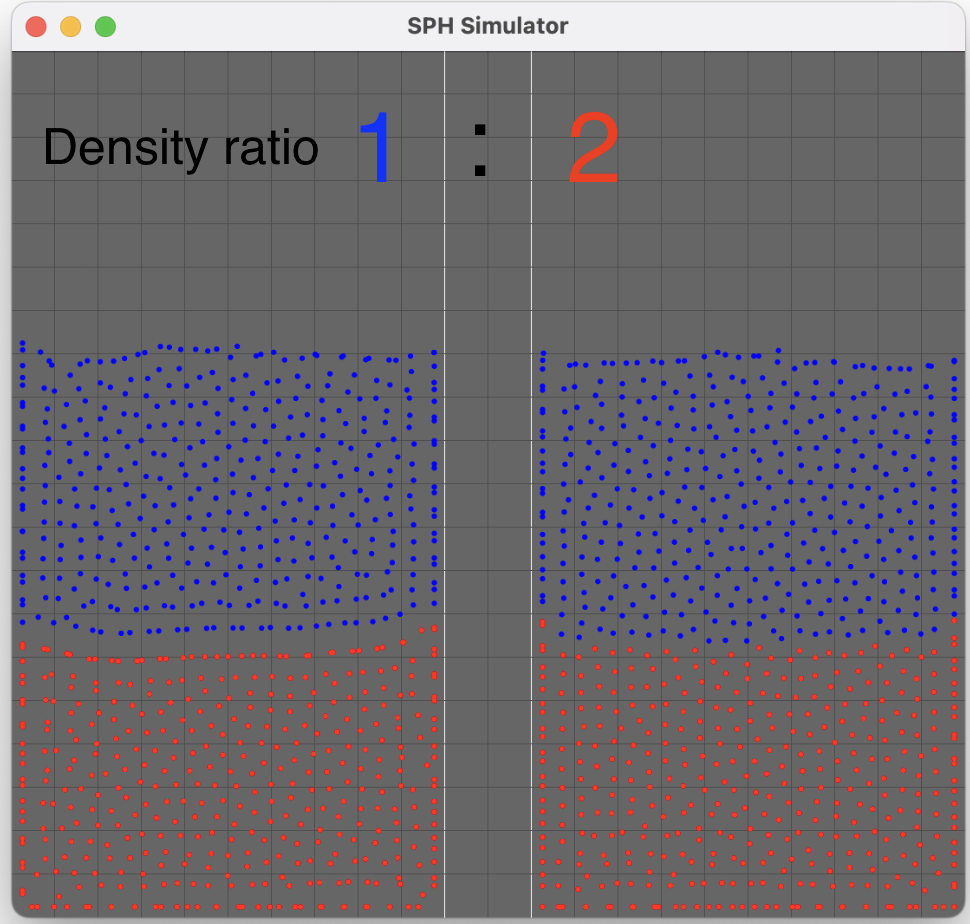
The new approach also enables the simulation of fluids with high density ratios without stability
problems compared to the standard SPH.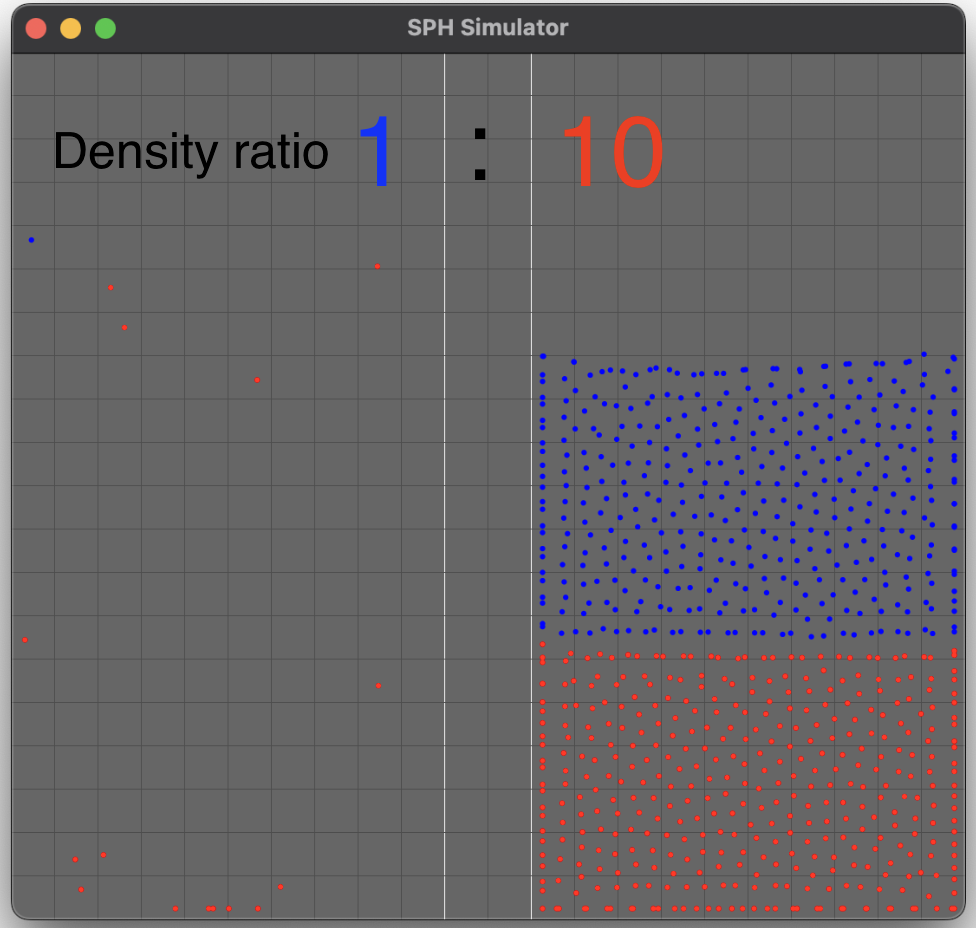
Ref: Solenthaler, Barbara, and Renato Pajarola. “Density contrast SPH interfaces.” (2008): 211-218.